Groupe de Travail d'Analyse Appliquée à Amiens - Février 2011

Résolution d'EDP en 2D avec

Introduction

FreeFem++ est un logiciel GRATUIT permettant de résoudre numériquement des EDP par éléments finis ; la géométrie du problème est définie par paramétrisation et l'écriture de la formulation variationnelle est proche de celle faite sur papier.

C'est un outil tout à fait intéressant pour les problèmes de taille moyenne. Il est également une aide à la modélisation dans le sens où il permet d'obtenir des résultats numériques rapidement ce qui se révèle utile pour modifier un modèle physique, pour dégager des directions d'investigation d'analyse mathématique etc ...

Le site officielle de FreeFem++ est :
www.freefem.org/ff++
Une documentation de FreeFem++ est accessible sur l'adresse suivante :
www.freefem.org/ff++/ftp/FreeFem++doc.pdf
Vous pouvez également télécharger l'interface graphique de FreeFem++ : FreeFem++-cs de l'adresse suivante :   www.ann.jussieu.fr/~lehyaric/ffcs/install.php
A la fin, pour la visualisation des données vous pouvez utiliser les logiciels Gnuplot : www.gnuplot.info/, Mathématica : http://www.wolfram.com/mathematica/ et Medit : www.ann.jussieu.fr/~frey/logiciels/Docmedit.dir/index.html


Présentation GTA3_FreeFem++_2D

Equation de Poisson




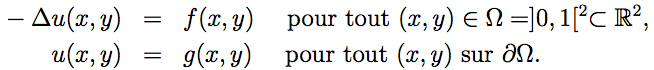
Code Solution
verbosity=0.;
real Dx=.01,Dy=.01;
mesh Th=square(floor(1./Dx),floor(1./Dy));
fespace Vh(Th,P1);
Vh uh,vh;
func f = 1.;
func g = 0.;
macro Grad(u)[dx(u),dy(u)]//
solve Poisson(uh,vh) = int2d(Th)(Grad(uh)'*Grad(vh))
                                   - int2d(Th)( f*vh) + on(1,2,3,4,uh=g) ;                
plot(uh,dim=2,fill=true,value=true,boundary=false);



Equation de la chaleur


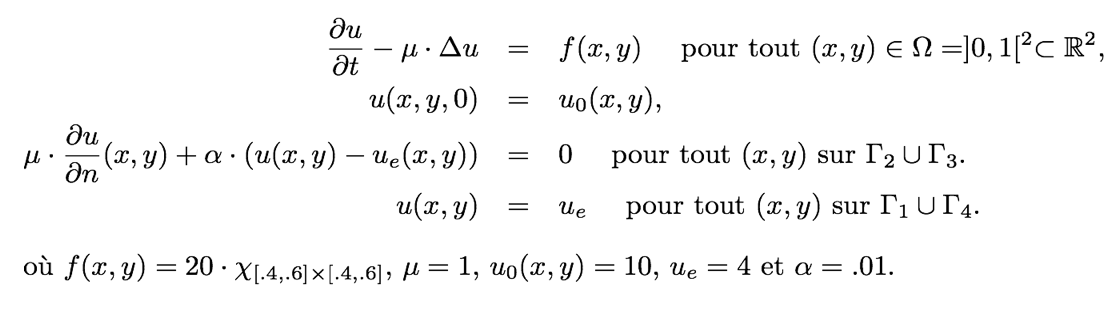
Code Solution
verbosity=0.;
real Dx=.02,Dy=.02;
mesh Th=square(floor(1./Dx),floor(1./Dy));
fespace Vh(Th,P1);
Vh uh,vh,uh0=10.;
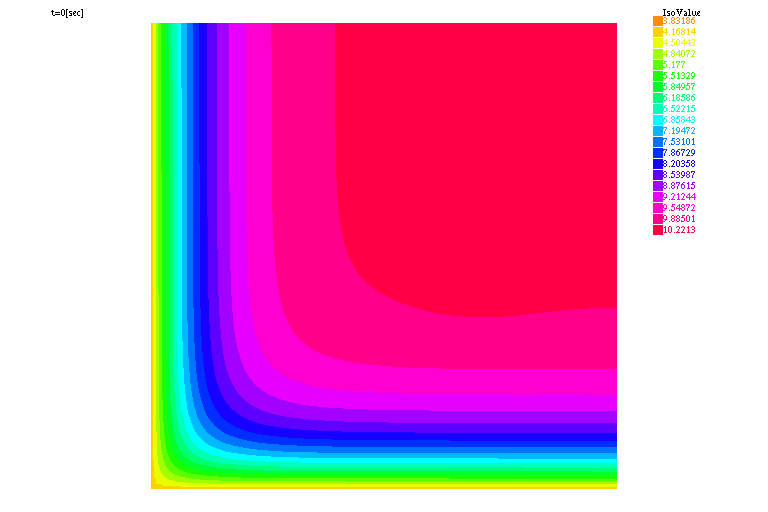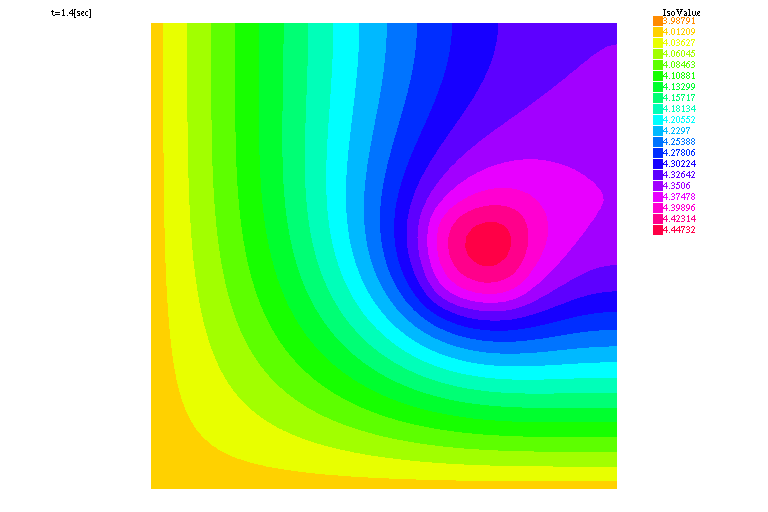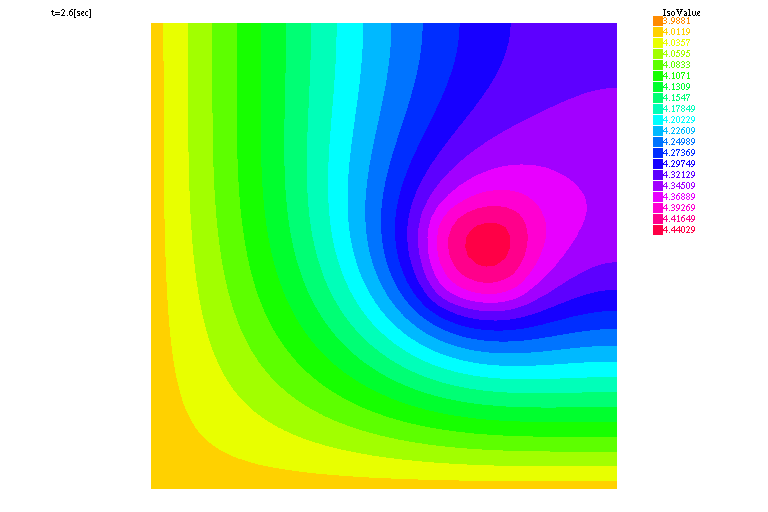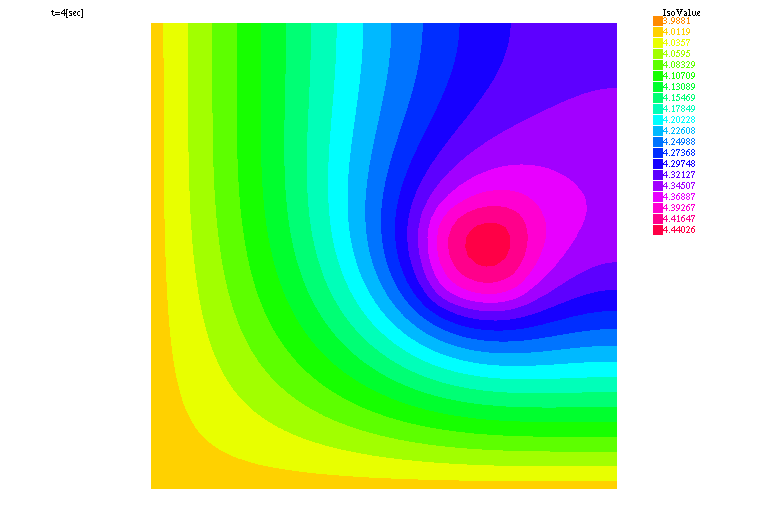
real ue = 4., mu = 1., alpha=.001, dt=0.01, Tf=10. ;
func f=20.*(.6<=x & x<=.8)*(.4<=y & y<=.6);
macro Grad(u)[dx(u),dy(u)]//
problem chaleur(uh,vh) = int2d(Th)(uh*vh/dt +  Grad(uh)'*Grad(vh)*mu) - int2d(Th)(uh0*vh/dt + f*vh)
                + int1d(Th,2,3)(uh*vh*alpha) - int1d(Th,2,3)(ue*vh*alpha)
                + on(1,4,uh=ue);
int kk=0;
for (real t=0.;t<Tf;t+=dt) {
    chaleur;
    uh0=uh;
    if ( !(kk % 20))   
        plot(uh,cmm="t="+t+"[sec]",dim=2,fill=true,value=true,wait=1);
    kk+=1;
}




Equation des Ondes



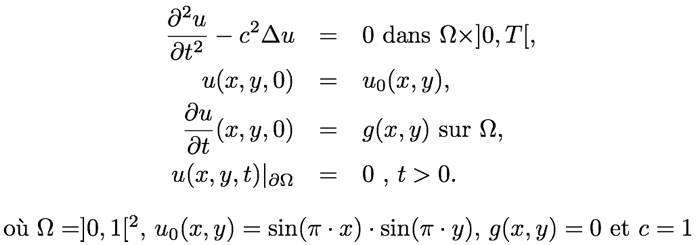
Code Solution
verbosity=0;
load "medit"
load "msh3"
real Dx=.02,Dy=.02;
mesh Th=square(floor(1./Dx),floor(1./Dy));
fespace Vh(Th,P1); 
func g=0.;
real c=1.,dt=.01,Tf=4.;
Vh uh,vh,uh0=sin(pi*x)*sin(pi*y),uh1=uh0+dt*g;
macro Grad(u)[dx(u),dy(u)]//
problem tambour(uh,vh) = int2d(Th)(uh*vh + Grad(uh)'*Grad(vh)*(c*dt)^2*.5 )
                    + int2d(Th)(Grad(uh0)'*Grad(vh)*(c*dt)^2*.5 )
                    - int2d(Th)(2.*uh1*vh - uh0*vh)
                    + on(1,2,3,4,uh=0);
int kk=0,k=0;
for (real t=0.;t<Tf;t+=dt) {
  tambour;
  uh0 = uh1;
  uh1 = uh;
  if ( !(kk % 20)){        plot(uh,cmm="t="+t,fill=true,value=true,wait=1,dim=3,boundary=false);
     // pour visualiser la solution avec Medit
     mesh3 TK=movemesh23(Th,transfo=[x,y,uh/2.]);
     medit("Solution",TK);
     savemesh(TK,"Ondes2D."+(100000+k)+".mesh");
     // pour visualiser la solution avec Mathématica
     { ofstream ff("Ondes2D."+(100000+k)+".txt");
     for (int i=0;i<Th.nt;i++){
        for (int j=0; j <3; j++)
           ff<<Th[i][j].x << " "<< Th[i][j].y<< " "<<uh[][Vh(i,j)]<<endl;
        ff<<Th[i][0].x << " "<< Th[i][0].y<< " "<<uh[][Vh(i,0)]<<"\n";
     }
     }
     k++;
  }
  kk++;
}
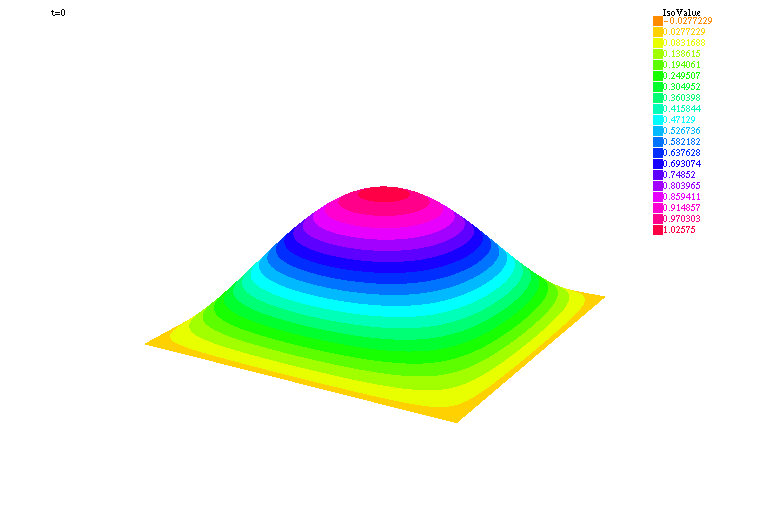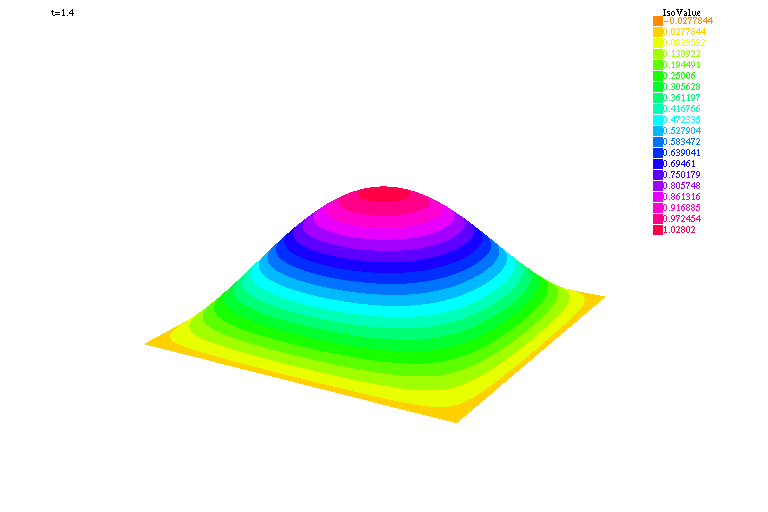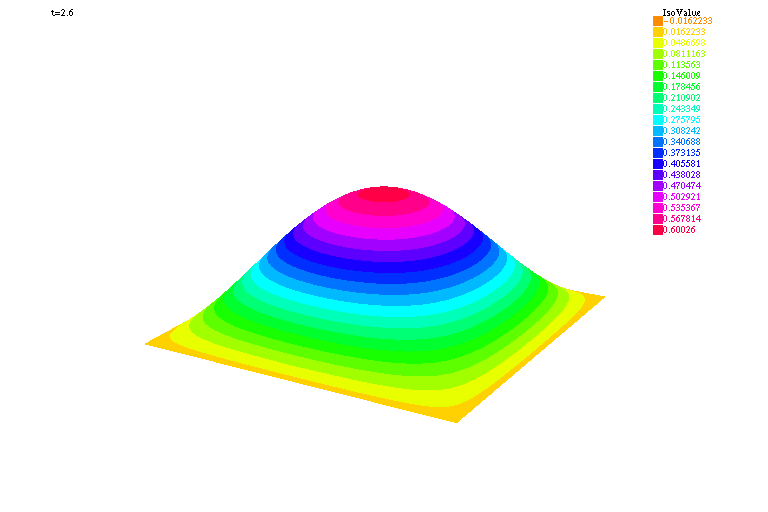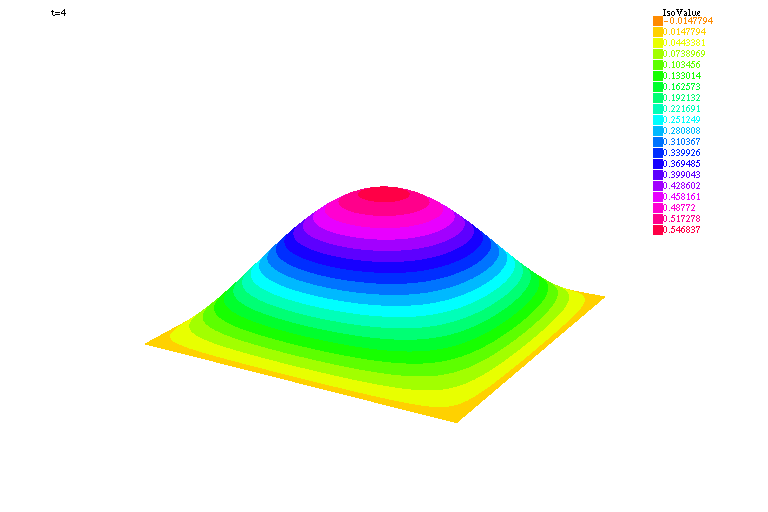Solution visualisée avec Mathématica

Solution visualisée avec Medit

           




Equation Elliptique Non Linéaire




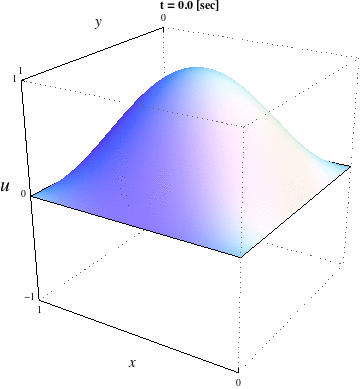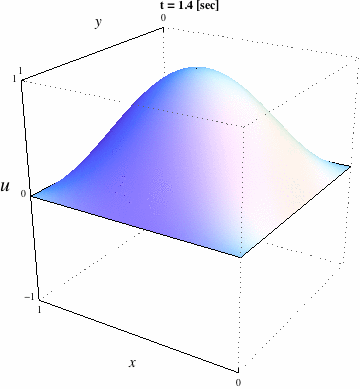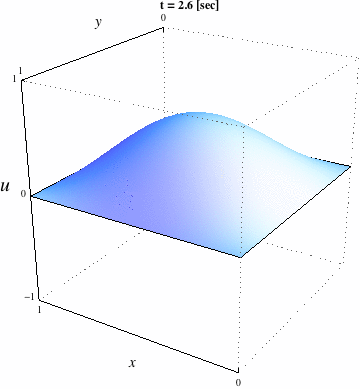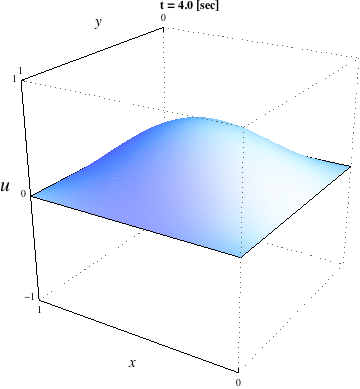
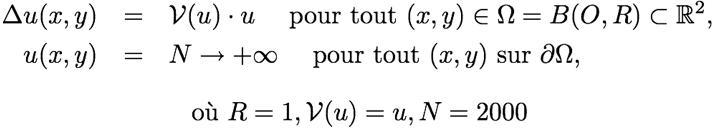
Code Solution
verbosity=0.;
real Dx=.02, R=1.;
border C(t=0.,2.*pi){x=R*cos(t);y=R*sin(t);label=1;};
mesh Th=buildmesh(C(floor(2.*pi*R/Dx)));
fespace Vh(Th,P1);
Vh uh, uh0=0, V=uh0, vh;
macro Grad(u)[dx(u),dy(u)]//
real N=2000.;
problem probdup(uh,vh) = - int2d(Th)(Grad(uh)'*Grad(vh))
          - int2d(Th) ( uh*V*vh ) + on(1,uh=N);
for (int i=0;i<=1000;i++) {
    probdup;
    V=uh;
    if (i%10==0) plot(uh,cmm="iter="+i+";min="+uh[].min+
";max="+uh[].max+";N="+N,fill=true,value=true,dim=3,
wait=1,boundary=false);
}




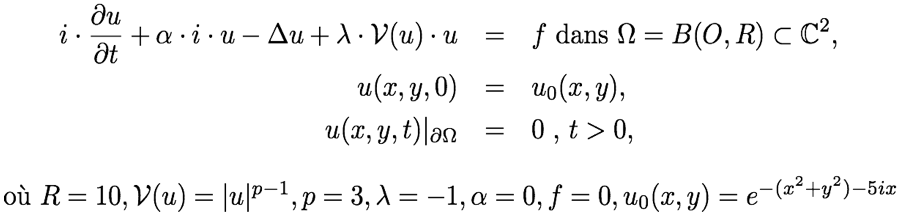
Equation Non Linéaire de Schrödinger





Code Solution
verbosity=0;
real Dx=.2, R=10.;
border C(t=0.,2.*pi){x=R*cos(t);y=R*sin(t);label=1;};
mesh Th=buildmesh(C(floor(2.*pi*R/Dx)));
fespace Vh(Th,P2);
real dt=0.01,Tf=10., lambda=-1., p=3.,alpha=0.;
Vh<complex> uh, vh, uh0=exp(-x^2-y^2-5.*1i*x), uhk=uh0, TNL, B;
varf a(u,v) = int2d(Th)(u*v*1i/dt + u*v*1i*alpha/2. + (dx(u)*dx(v) + dy(u)*dy(v))/2.) + on(1,u=0);
matrix<complex> A = a(Vh,Vh);
varf b(u,v) = int2d(Th)(uh0*v*1i/dt - uh0*v*1i*alpha/2. - (dx(uh0)*dx(v) + dy(uh0)*dy(v))/2. - lambda*TNL*(uhk+uh0)*v/2.) + on(1,u=0);
Vh ABSU;
int kk=0;
real[int] NORML2(floor(Tf/dt)+1);
for (real t=0.;t<=Tf;t+=dt){
    TNL=abs(uh0)^(p-1);
     for (int i=0;i<2;i++){
        B[] = b(0,Vh);
        set(A,solver=sparsesolver);
        uhk[] = A^-1*B[];
    }
    uh0[]=uhk[];
    ABSU=abs(uh0);
    NORML2[kk]=sqrt(int2d(Th)(abs(uh0)^2));       
    if ( !(kk % 10)){
        plot(ABSU,cmm="t="+t+"  ;||u||_L^2="+NORML2[kk], fill=true,value=true,dim=2);
    {
        ofstream gnufile("||u||_L2.gnu");
         for (int i=0;i<=kk;i++)
            gnufile<<i*dt<<" "<<NORML2(i)<<endl;
    }
exec("echo 'plot \"||u||_L2.gnu\" w lp \
pause 5 \
quit' | gnuplot");
    }
    kk++;
}
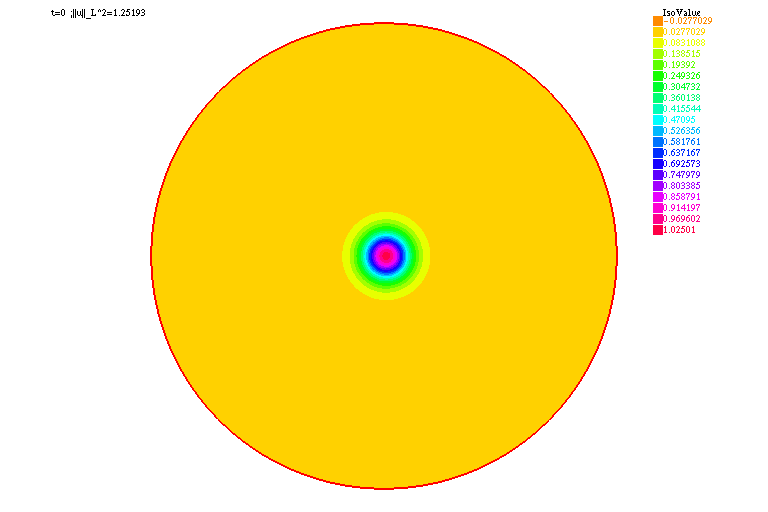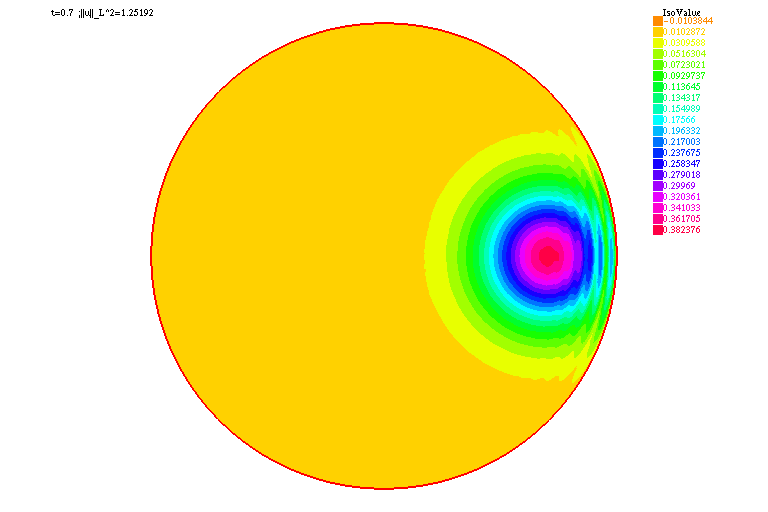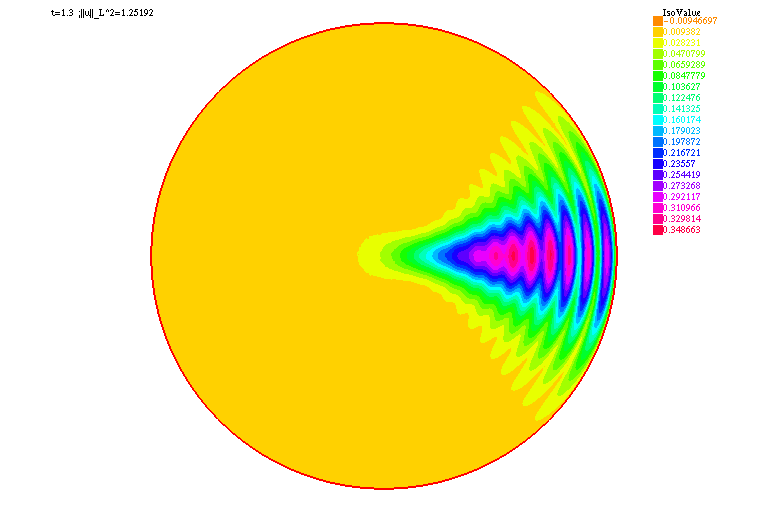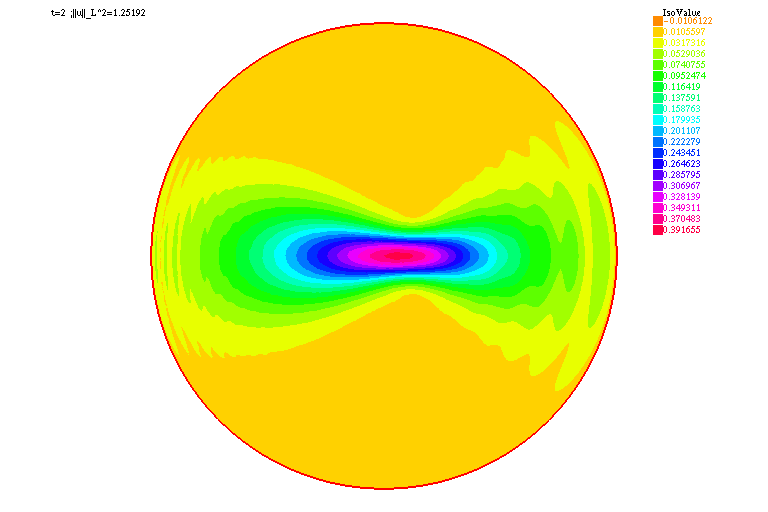